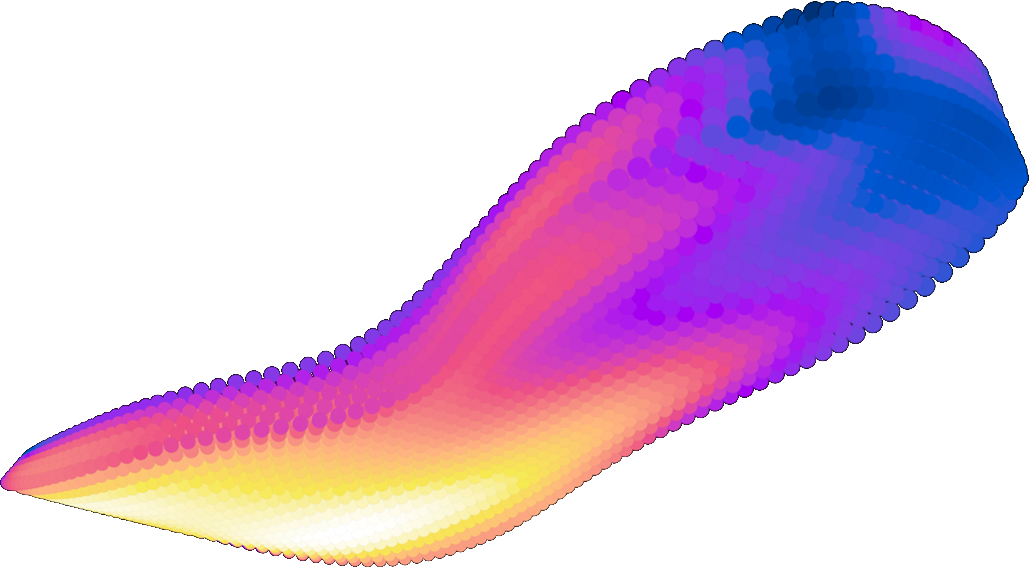

Pressure data informs the design of sneakers and is used to modulate the material distribution across the midsole and the upper through changes in topology and density.
As part of a workshop on shoe design offered by New Balance at MIT, led by Onur Yuce Gun and Chris Wawrousek, I had access to pressure data collected between the instep and the midsole and the outsole as well as to in-plane strain data on the upper, which was collected via high-frequency imaging.
Unfortunately, the data was not temporal: it had been measured across multiple strides and averaged. In addition, it had been averaged and normalized. In fact, the strain data was provided as provided as a texture mapped on a mesh. My guess is that New Balance has access to high-quality data but decided not to share it for confidentiality purposes. Still, it was great to have access to any sort of measured data.
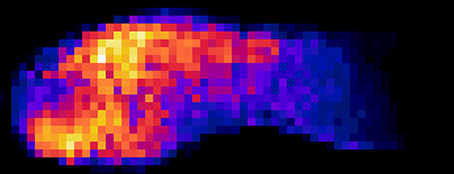

Because the pressure and strain data was fairly noisy and had low spatial resolution, I mapped the pressure to a parametric surface representing the midsole and then built smooth, non-linear regression models, that would provide information at a high spatial resolution, which was needed since I planned on sampling the pressure values throughout the surface to inform the material distribution. The model would also provide interpolated values throughout the interior of the midsole.
The bonus side-effect: I can control the level of smoothness of my model by tuning its hyperparameters. I used kernel ridge regression, so I was able to tune both the polynomial degree and regularization coefficient. This is a great way to drive whether a material distribution design will be extreme—it will be informed closesly by the pressure data, which could be useful for high-performance applications where the range of movements is well-studied—or whether it will be more evenly distributed, which could be better suited for versatile applications and casual wear.

I used a similar approach for the strain data on the upper, with the added challenge that I had to first reverse-engineer the color scale used for the texture data. I also had to map the texture data from the mesh to the NURBS surface representing the upper. I made the model smoother to obtain better distributed support in the end.

Unsurprisingly, the largest strains occur right at the toe joints. This is where the upper should be as flexible as possible. In contrast, at the heel, the upper should provide more support.
I chose that I would use the regression model as a way to inform both the topology and the density of cells in the midsole and to control the surface shape and aperture density in the upper. It was hypothesized that high-pressure regions in the midsole would require more support and so would low-strain areas in the upper. Conversely, high-strain areas in the upper should be flexible.
These principles led me through a few design iterations. The frist relied on discontinous topological changes. While I find the results interesting, I was not satisfied with the resulting aesthetics of the midsole, and I was also skeptical as to how that would perfom. This was also a lost opportunity to take advantage of the high-resolution models I had built.


As a result, I decided to vary density, topology, and geometry continuously throughout the entire shoe based on the pressure and strain models. There as still a lot of freedom in deciding exactly how the model would map to geometry and topology, and I generated a few different sneakers designs below, the first one being my favorite.





Finally, the models were 3D-printed at New Balance.



